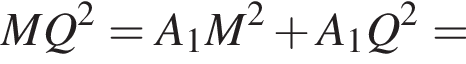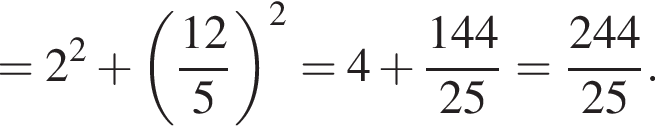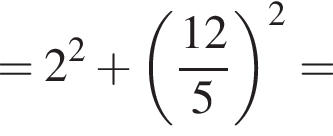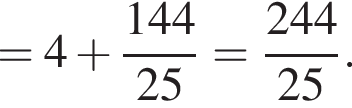i
Многогранник ABCA1B1C1 — правильная треугольная призма, все ребра которой равны 6. Точки P и K — середины ребер B1C1 и CC1 соответственно, M ∈ AA1, A1M : A1A = 1 : 3 (см. рис.). Найдите увеличенный в 25 раз квадрат длины отрезка, по которому плоскость, проходящая через точки M, K, P, пересекает грань AA1B1B.
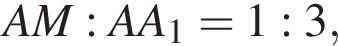то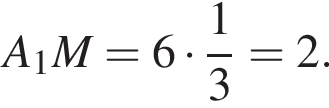 
Треугольники PC1K и LB1P равны по стороне и двум прилежащим к ней углам, тогда 
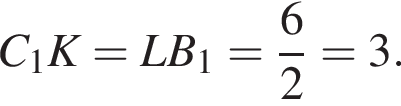Треугольники LQB1 и A1MQ подобны по двум углам, откуда 
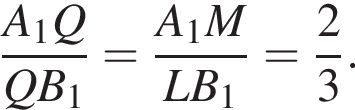Пусть длина отрезка A1Q равна 2x, тогда длина отрезка QB1 равна 3x. Так как длина ребра A1B1 равна 6, получаем, что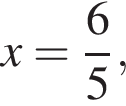 
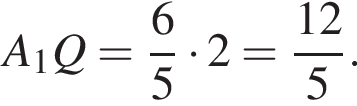По теореме Пифагора в треугольнике A1MQ:
